線形回帰
線形回帰はいろいろなサイトで説明がありますが,それぞれ推定したバラメータの分散・標準偏差・標準誤差,についてはあまり詳しく書かれていません.
そこで,ここのサイトを全面的に(ほぼコピー)させていただいて,自分の備忘録として残すことにしました.ありがとうございます.
目標は,
線形回帰の場合の各パラメータの誤差
ですが,ゆくゆくは,
非線形回帰の場合の各パラメータの誤差
を求めて行きたいと思っています(まだまだ先が長そうですが).
単回帰
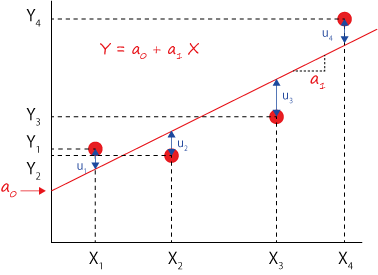
n個の点,\(\Large \displaystyle (X_1, Y_1), (X_2, Y_2), .......(X_n, Y_n), \),があり,各結果には誤差が含まれています.
これを切片を持つ直線で近似する場合を考えます.近似式は,
\(\Large \displaystyle Y_i = a_0 + a_1 X_i \)
となります.ここで,a0が切片,a1が傾きとなります.

α,βの推定値を求めるのが目的なので,各パラメータの推定値を,
\(\Large \displaystyle \hat{a_0}, \hat{a_1} \)
とすると,
\(\Large \displaystyle Y_i = \hat{a_0} + \hat{a_1} X_i + \hat{u_i} \)
と記します.ここで,uiはi番目のYiと推定結果との誤差となります(なぜuにもhatがかかるかは疑問ですが...たぶん,各パラメータは推定値なのでそれに対する誤差も推定値,という意味かと)
ここで前提として,Xiは誤差を含まないもの,Yiは実験誤差などを含むものとして考えます.
この,\(\Large \displaystyle \hat{u_i}^2 \)が最小値をとる\(\Large \displaystyle \hat{a_0}, \hat{a_1} \)を推定すればいいので,
\(\Large \displaystyle S \left( \hat{a_0}, \hat{a_1} \right) = \sum_{i=1}^{n} \hat{u_i}^2 = \sum_{i=1}^{n} \left( Y_i - \hat{a_0} - \hat{a_1} X_i \right)^2 \)
が最小値をとる\(\Large \displaystyle \hat{a_0}, \hat{a_1} \)を求めます.これを,最小二乗法,と呼びます.
最小値を求めるには各パラメータで微分した値が0となればいいので,
\(\Large \displaystyle \frac{ \partial S \left( \hat{a_0}, \hat{a_1} \right) }{ \partial \hat{a_0} } = 0 \)
\(\Large \displaystyle \frac{ \partial S \left( \hat{a_0}, \hat{a_1} \right) }{ \partial \hat{a_1} } = 0 \)
を計算すればいいことになります.